Tapered Bores and Standing Waves
Tapered bores started to appear in flutes around 1700. Apparently it was discovered empirically that this helped address some of the tuning deficiencies of the cylindrical Renaissance flute. No written records of a theory of tapering exist (if there even was one). All we can do is examine the instruments that have survived from that period. It has been known for a long time that sticking wax into the bore of a flute will change the pitch. In fact, the regulators on Uillean pipes are made with a long pin in the bore onto which pieces of wax can be attached for fine-tuning. We can speculate that the tapered flute bore may have evolved from such experiments.
More recently, physicists like Arthur Benade developed mathematical models for calculating the effect of bore tapers. In Chapter 22 of his excellent book Fundamentals of Musical Acoustics [Benade2] Benade gives an intuitive explanation of how bore changes affect pitch. I reproduce a couple of key figures here (by kind permission of Dover Books). First, he shows the pressure standing waves that form inside the flute:
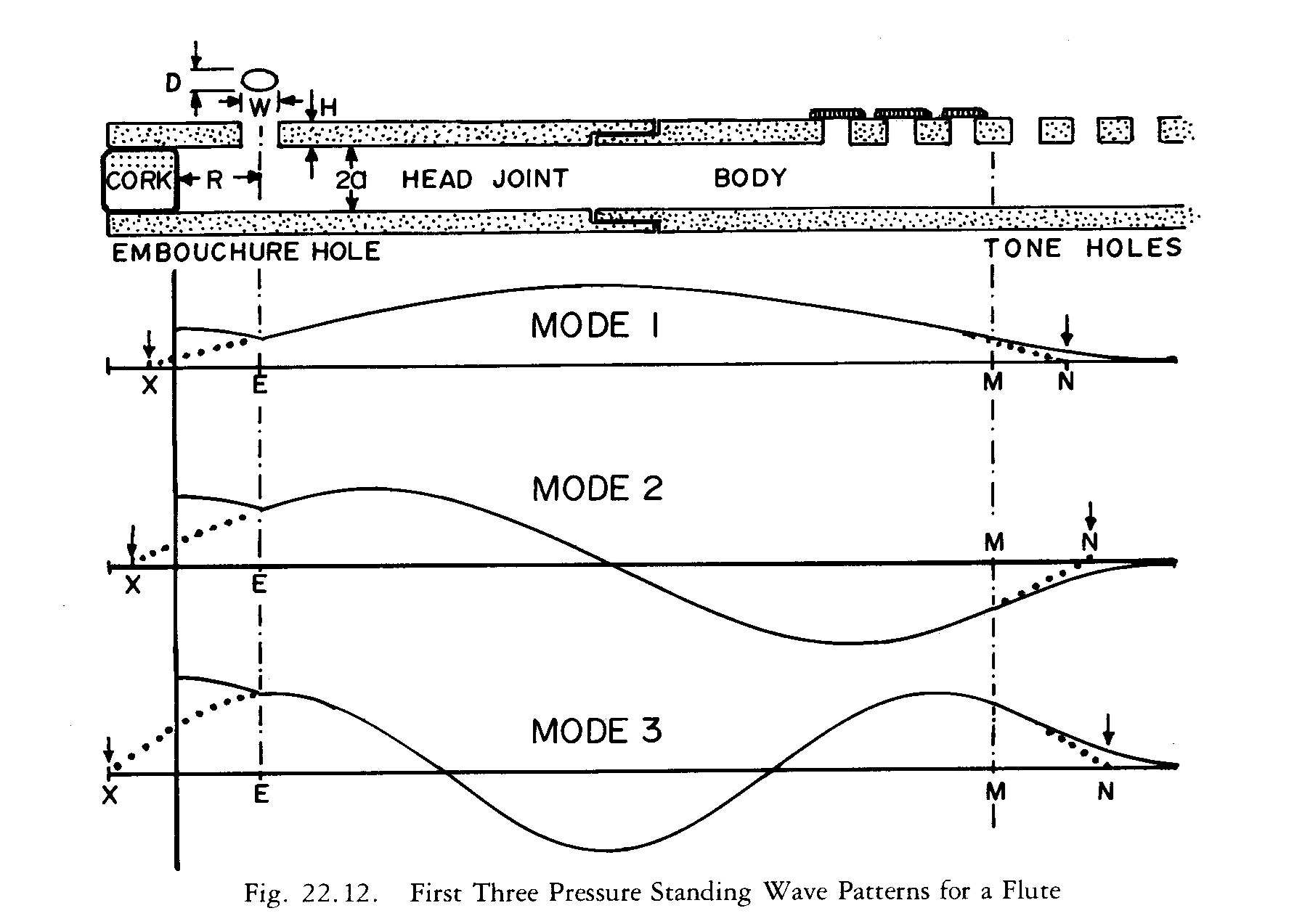
W Curves
Then he explains that a constriction in the bore will sharpen a note if it is at a pressure maximum, but flatten it if it is at a pressure minimum. He shows this graphically with something he calls W curves:

These curves tell you what the effect of a change in the bore will be for a particular bore location and note. It is clear from looking at these curves that there is an important practical difference between head tapers and body tapers. Head tapers affect all of the notes. On the other hand, the part of a body taper that is below an open tone hole has less effect on that note. That means one could create a taper by moving down from the top tone hole and shrinking each section of bore between tone holes successively for best effect on the next lowest hole. I can imagine the conical bore profile might have evolved by such an empirical process.
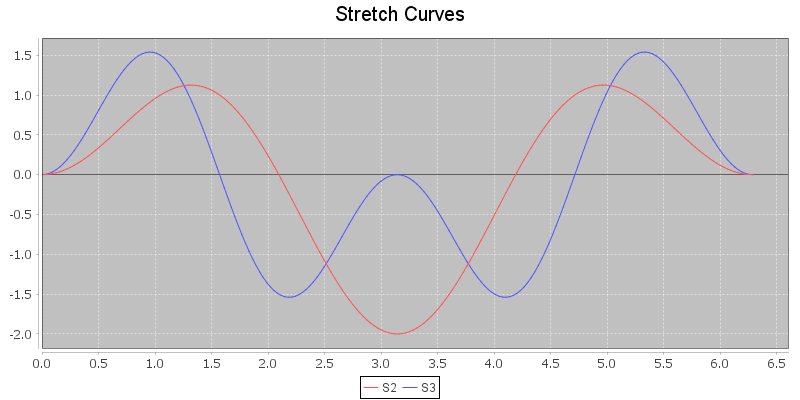
S Curves
Cylindrical flutes have a flat second octave. The bore taper stretches the octave to correct this. I am particularly interested in octave stretch for this reason. The W curves show pitch changes; I had the idea that one could make
a similar curve to show octave stretch changes. I call these S (or Stretch) curves, and they are calculated by subtracting W curves to show the difference in pitch change between octaves, e.g. S2 = W2 - W1, S3 = W3 - W1. S Curves look like this:
| 
