Benade's Bore Perturbation Calculation
In 1965 Benade and French wrote "Analysis of the Flute Head Joint" [Benade1] which (among other things) presented a method of analysing the effect of head taper on pitch and then applied the method to measurements of several Boehm-style flute headjoints. Benade had developed a model using transmission line equations to model the flute bore, and this method was a simplification of that. The method was also presented in a qualitative way in Chapter 22 of Fundamentals of Musical Acoustics [Benade2] which I describe here. It is analogous to a Fourier transform, where the internal standing waves are multiplied by the bore changes. The equation is:
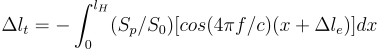
| Δlt | Change in acoustic bore length |
| lH | Length of the head joint |
| Sp | Perturbation to bore cross section |
| S0 | Bore cross section |
| f | Frequency |
| c | Speed of sound |
| Δle | Embouchure correction |
The equation gives the effective change in acoustic length for a given frequency. Adding this to the original length allows calculation of the new frequency. The Sp/S0 term is the change in area divided by the original area--the change in area as a fraction. This means that if a bore profile has its areas multiplied by a constant, this equation will produce the same result. Because of this, it is a good idea to define models is such a way that they preserve the aspect ratio of the bore. Benade held the body diameter constant in a tapered head model; similarly, one could hold the head diameter constant in a conical bore model.
Since B+F were only concerned with Boehm-style flute headjoints, the upper limit of the integral was the length of the head joint, as the rest of the bore was cylindrical. As illustrated here, the W Curves extend to the relevant open tone hole, so to make this work for body tapers we need to extend the integration limit. A limitation of this approach is that it assumes a bore perturbation below the tone hole has no effect, which we know is not the case.
| 
